Maths & Malices .
net
Une revue électronique,
culturelle et mathématique
|

|
|
|
Sixième livre proposition II
(Le théorème dit de Thalès)
Que l'on mène une droite parallèle à
un des côtés d'un triangle, cette droite
coupera proportionnellement les côtés de
ce triangle ; et si les côtés du triangle
sont coupés proportionnellement, la droite qui
joindra les sections sera parallèle au côté
restant du triangle.
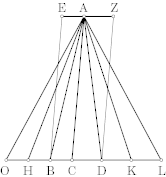
Menons DE parallèle à un des côtés
BC du triangle ABC ; je dis que BD est à DA comme
CE est à EA. Joignons BE, CD.
|
|
|
Le triangle BDE sera égal au triangle CDE (prop.
37. I), parce qu'ils ont la même bas DE, et qu'ils
sont compris entre les mêmes parallèles DE,
BC. Mais ADE est un autre triangle ; et des grandeurs égales
ont la même raison avec une même grandeur ;
donc le triangle BDE est au triangle ADE comme le triangle
CDE est au triangle ADE. Mais le triangle BDE est au triangle
ADE comme BD est à DA ; pour ces deux triangles,
qui ont la même hauteur, savoir, la perpendiculaire
menée du point E sur la droite AB, sont entr'eux
comme leurs bases (prop. 1. VI). Par la même raison
le triangle CDE est un triangle ADE comme CE est à
EA ; donc BD est à DA comme CE est à EA (prop.
11. III).
Mais que les côtés AB, AC du triangle ABC
soient coupés proportionnellement aux point D, E,
c'est-à-dire que BD soit à DA comme CE est
à EA, et joignons DE ; je dis que DE est parallèle
à BC.
|
|
|
Faisons la même construction. Puisque BD est à
DA comme CE est à EA, que BD est à DA comme
le triangle BDE est au triangle ADE (prop. 1. VI), et que
CE est à EA comme le triangle CDE est au triangle
ADE, le triangle BDE est au triangle ADF comme le triangle
CDE est au triangle ADE (prop. 11. V). Donc chacun des triangles
BDE, CDE à la même raison avec le triangle
ADE. Donc les triangles AHB, ABC sont égaux entr'eux
(prop. 38. I) ; donc le triangle AOC est le même multiple
du triangle ABC que la base OC l'est de la base BC. Par
la même raison, le triangle ADC est le même
multiple du triangle ACD que la base CL l'est de la base
CD. Donc si la base OC est égale à la base
CL, le triangle AOC est égal au triangle ALC ; si
la base OC surpasse la base CD, le triangle AOC surpasse
le triangle ALC (prop. 38. I); et si la base OC est plus
petite que la base CL, le triangle AOC est plus petit que
le triangle ALC. Ayant donc quatre grandeurs, les deux bases
BC ,CD ; et les deux triangles ABC, ACD, on a pris des équimultiples
quelconques de la base BC, et du triangle ABC, savoir, la
base OC et le triangle AOC ; on a pris aussi d'autres équimultiples
quelconques de la base CD et du triangle ACD, savoir, la
base CL et le triangle ALC ; et l'on a demontré que
si la base OC surpasse la base CL, le triangle AOC surpasse
le triangle ALC ; que si la base OC est égale à
la base CL, le triangle AOC est égal au triangle
ALC, et que si la base OC est plus petite que la base CL,
le triangle AOC est plus petit que le triangle ALC ; donc
la base BC est à la base CD comme le triangle ABC
est au triangle ACD (déf. 6. VI).
|
|
Puisque le parallélogramme EC est double du triangle
ABC, que le parallélogramme ZC est double aussi du
triangle ACD (prop.41.1), et que les parties ont entr'elles
la même raison que leurs équimultiples (prop.15
5), le triangle ABC est au triangle ACD comme le parallélogramme
EC est au parallélogramme ZC. Puisqu'on a dÈmontrÈ
que la base BC est ý la base CD comme le triangle ABC est
au triangle ACD, et puisque le triangle ABC est au triangle
AC comme le parallélogramme EC est au parallélogramme
ZC, la base BC est la base CD comme le parallélogramme
EC est au parallélogramme ZC (prop. 11. V). Donc,
etc.
BDE est égal au triangle CDE (prop. 9. V) ; et
ils sont sur la même base DE. Mais les triangles égaux
et construits sur la même base sont entre les même
parallèles (prop. 39. I). Donc DE est parallèle
à BC.
Donc, etc.
|
|
|
|
|
